我们知道,有理数不是数的终点,有理数之外还有实数和虚数,虚数和实数可以组成复数。复数是科学运算中常用的到的数学概念,而python是科学运算中常用的编程语言,所以python对科学运算的支持是很好的(将复数内置在了标准库中,可以直接使用)。接下来就让我们来看看python复数表示和复数运算是怎么操作的吧。
前言
复习试题时,发现一道复数问题
问题
关于 Python 的复数类型,以下选项中描述错误的是
A复数的虚数部分通过后缀“J”或者“j”来表示
B对于复数 z,可以用 z.real 获得它的实数部分
C对于复数 z,可以用 z.imag 获得它的实数部分
D复数类型表示数学中的复数
正确答案: C
首先我们来明确一下什么是复数: 复数在数学上面的定义是由实数部分和虚数部分所组成的数,形如a+bj .
其中a、b为实数,j为“虚数单位”,j 的平方等于-1.a、b分别叫做复数a+bj的实部和虚部。
下面让我们在Python中定义一个复数:real + imag(虚部的单位可以是j或者J)
a = 6 + 0.6j# 输出这个复数a
print(a)# 获取实部
print(a.real)# 获取虚部
print(a.imag)# 获取该复数的共轭复数
print(a.conjugate())# 让我们通过complex函数来定义一个复数
a = complex(1, 2)
b = complex(1)
c = complex("1")
d = complex("1+2j")
# 运行结果
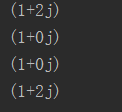
补充:Python 复数及运算类型问题
在做题的时候遇到了这样的问题:
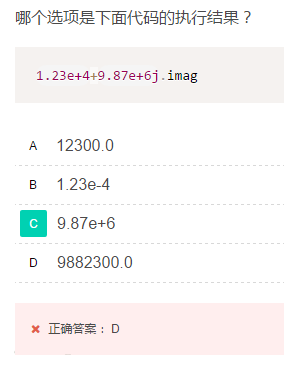
按照数学上的知识,我们通常会认为实部是1.23e+4,也就是12300;虚部是9.87e+6,也就是9870000。
但是程序运行结果却不是这样:

为什么和我们想象的不一样呢,这里面涉及到两个问题:
1、实部虚部问题
2、结果类型问题
再来看一些例子:
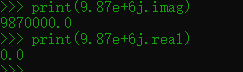
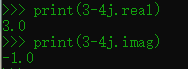
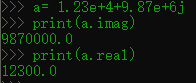
通过上述例子可以看出,如果我们使用<复数>.<imag>的方式来获取虚部,那么计算机就会将这个复数的实部和虚部相加,并且以浮点数的类型返回。而如果要获取我们通常理解意义上的虚部,则要将这个复数赋给一个变量,通过<变量>.<imag>的方式获取,就能得到“a + bi”模式的虚部。

实部的获取相对容易理解,不是紧跟 j 的就是实部,同样以浮点数的类型返回。
另一个问题就是运算类型的问题,Python中有三种数据类型:整数、浮点数、复数。这三种类型数据混合参与运算时,结果的类型采用“最宽范围”的类型,复数类型范围最宽,整数最窄。
在上述例子中,复数的实部、虚部不会是复数类型,则以次于复数类型的浮点数类型返回。
再列出一些运算的例子:
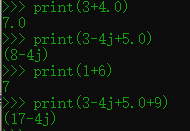
当然,如果类型保持一致,则以同样类型返回运算结果(类型一致也就是最宽的类型就是他本身的类型)。
以上就是python复数运算和复数表示的全部内容,希望对大家的学习有所帮助,也希望大家多多支持W3Cschool。

 免费AI编程助手
免费AI编程助手



