在一些编辑算法中,我们可能会需要对一个二维数组(更准确的称呼应该为:矩阵)的某个区域进行取值计算,在特定区域取完值后我们需要移动到下一个区域。我们把这个区域称之为窗口,移动这个区域我们又叫它移动窗口。numpy作为一个出名的科学计算的库,它提供了矩阵运算的支持,所以他也提供了移动窗口这种操作接下来这篇文章我们就来了解一下python在numpy上移动窗口怎么操作吧!
简介
今天很有可能你已经做了一些使用滑动窗口(也称为移动窗口)的事情,而你甚至不知道它。例如:许多编辑算法都是基于移动窗口的。
在GIS中做地形分析的大多数地形栅格度量(坡度、坡向、山坡阴影等)都基于滑动窗口。很多情况下,对格式化为二维数组的数据进行分析时,都很有可能涉及到滑动窗口。
滑动窗口操作非常普遍,非常有用。它们也很容易在Python中实现。学习如何实现移动窗口将把你的数据分析和争论技能提升到一个新的水平。
什么是滑动窗?
下面的例子显示了一个3×3(3×3)滑动窗口。用红色标注的数组元素是目标元素。这是滑动窗口将计算的新度量的数组位置。例如,在下面的图像中,我们可以计算灰色窗口中9个元素的平均值(平均值也是8),并将其分配给目标元素,用红色标出。你可以计算最小值(0)、最大值(16)或其他一些指标,而不是平均值。对数组中的每个元素都这样做。
就是这样。这就是滑动窗口的基本原理。当然,事情可能变得更加复杂。有限差分方法可以用于时间和空间数据。逻辑可以实现。可以使用更大的窗口大小或非正方形窗口。你懂的。但在其核心,移动窗口分析可以简单地总结为邻居元素的平均值。
需要注意的是,必须为边缘元素设置特殊的调整,因为它们没有9个相邻元素。因此,许多分析都排除了边缘元素。为简单起见,我们将在本文中排除边缘元素。

样例数组
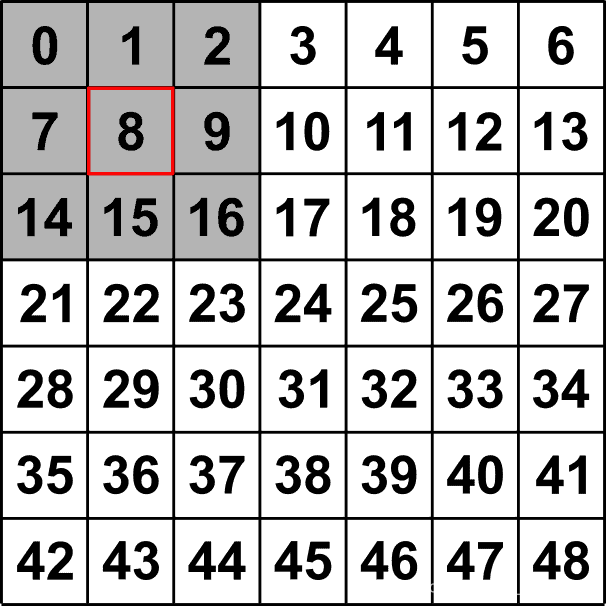
3x3的滑动窗口
创建一个NumPy数组
为了实现一些简单的示例,让我们创建上面所示的数组。首先,导入numpy。
import numpy as np
然后使用arange创建一个7×7的数组,值范围从1到48。另外,创建另一个包含无数据值的数组,该数组的形状和数据类型与初始数组相同。在本例中,我使用-1作为无数据值。
a = np.arange(49).reshape((7, 7))
b = np.full(a.shape, -1.0)
我们将使用这些数组来开发下面的滑动窗口示例。
通过循环实现滑动窗口
毫无疑问,你已经听说过Python中的循环很慢,应该尽可能避免。特别是在使用大型NumPy数组时。这是完全正确。尽管如此,我们将首先看一个使用循环的示例,因为这是一种简单的方法来概念化在移动窗口操作中发生的事情。在你通过循环示例掌握了概念之后,我们将继续使用更有效的向量化方法。
要实现移动窗口,只需循环遍历所有内部数组元素,识别所有相邻元素的值,并在特定的计算中使用这些值。
通过行和列偏移量可以很容易地识别相邻值。3×3窗口的偏移量如下所示。
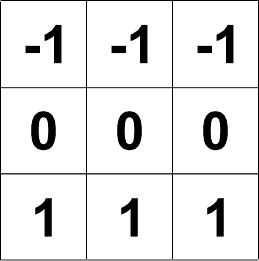
行偏移
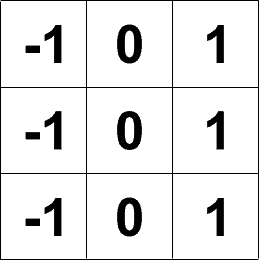
列偏移
循环中NumPy移动窗口的Python代码
我们可以用三行代码实现一个移动窗口。这个例子在滑动窗口内计算平均值。首先,循环遍历数组的内部行。其次,循环遍历数组的内部列。第三,在滑动窗口内计算平均值,并将值赋给输出数组中相应的数组元素。
for i in range(1, a.shape[0]-1):
for j in range(1, a.shape[1]-1):
b[i, j] = (a[i-1, j-1] + a[i-1, j] + a[i-1, j+1] + a[i, j-1] + a[i, j] + a[i, j+1] + a[i+1, j-1] + a[i+1, j] + a[i+1, j+1]) / 9.0
循环后结果
你将注意到结果与输入数组具有相同的值,但是外部元素没有被分配数据值,因为它们不包含9个相邻元素。
[[-1. -1. -1. -1. -1. -1. -1.] [-1. 8. 9. 10. 11. 12. -1.] [-1. 15. 16. 17. 18. 19. -1.] [-1. 22. 23. 24. 25. 26. -1.] [-1. 29. 30. 31. 32. 33. -1.] [-1. 36. 37. 38. 39. 40. -1.] [-1. -1. -1. -1. -1. -1. -1.]]
向量化滑动窗口
Python中的数组循环通常计算效率低下。通过对通常在循环中执行的操作进行向量化,可以提高效率。移动窗口矢量化可以通过同时抵消数组内部的所有元素来实现。
如下图所示。每个图像都有相应的索引。你将注意到最后一张图像索引了所有内部元素,并且对应的图像索引了每个相邻元素的偏移量。



从左到右的偏移索引:[1:-1,:-2],[1:-1,2:],[2 :, 2:]



从左到右的偏移索引:[2 :,:-2],[2 :, 1:-1],[:-2,1:-1]



从左到右的偏移索引:[:-2,2:],[:-2,:-2],[1:-1、1:-1]
Numpy数组上的向量化移动窗口的Python代码
有了上述偏移量,我们现在可以轻松地在一行代码中实现滑动窗口。 只需将输出数组的所有内部元素设置为根据相邻元素计算所需输出的函数。
b[1:-1, 1:-1] = (a[1:-1, 1:-1] + a[:-2, 1:-1] + a[2:, 1:-1] + a[1:-1, :-2] + a[1:-1, 2:] + a[2:, 2:] + a[:-2, :-2] + a[2:, :-2] + a[:-2, 2:]) / 9.0
矢量化滑动窗口结果
如你所见,这将得到与循环相同的结果。
[[-1. -1. -1. -1. -1. -1. -1.] [-1. 8. 9. 10. 11. 12. -1.] [-1. 15. 16. 17. 18. 19. -1.] [-1. 22. 23. 24. 25. 26. -1.] [-1. 29. 30. 31. 32. 33. -1.] [-1. 36. 37. 38. 39. 40. -1.] [-1. -1. -1. -1. -1. -1. -1.]]
速度比较
上述两种方法产生相同的结果,但哪一种更有效?我计算了从5行到100列的数组的每种方法的速度。每种方法对每个测试100次。下面是每种方法的平均时间。
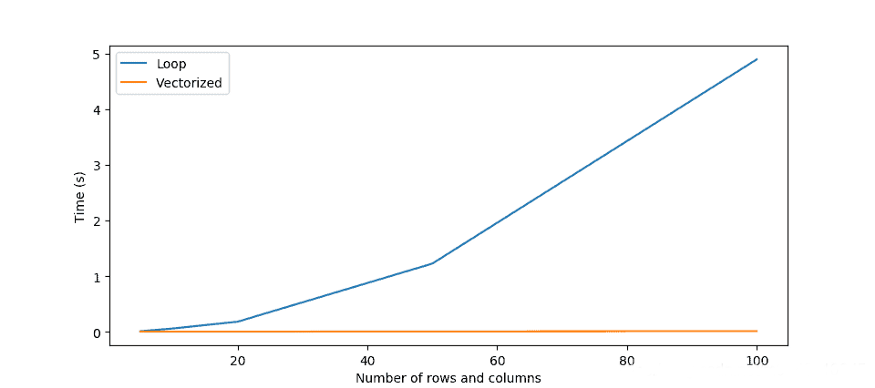
很明显,向量化的方法更加有效。随着数组大小的增加,循环的效率呈指数级下降。另外,需要注意的是,一个包含10,000个元素(100行和100列)的数组非常小。
总结
移动窗口计算在许多数据分析工作流程中非常常见。这些计算是非常有用的,非常容易实现。然而,使用循环来实现滑动窗口操作是非常低效的。
向量化的移动窗口实现不仅更高效,而且使用更少的代码行。一旦掌握了实现滑动窗口的向量化方法,就可以轻松有效地提高工作流程的速度。
补充:Python学习笔记——Numpy数组的移动滑窗,使用as_strided实现
Numpy中移动滑窗的实现
为何需要移动滑窗
在量化投资分析过程中,对历史数据进行分析是一个必不可少的步骤。滑窗在历史数据分析中的重要性不言而喻。譬如移动平均、指数平滑移动平均、MACD、DMA等等价格指标的计算都无一例外需要用到滑窗。
作为一种非常受欢迎的数据分析工具,pandas中提供了专门的滑窗类:DataFrame.rolling()。通过这个滑窗类,可以非常容易地实现移动平均等等算法,但是,在某些情况下,Pandas的运行速度还是不够,需要借助Numpy的高效率进一步提升速度,这时候就需要在Numpy中实现滑窗了。
Numpy中的移动滑窗
可惜Numpy并没有提供直接简单的滑窗方法,如果使用for-loop来实现滑窗,不仅效率打折扣,而且内存占用也非常大。实际上,Numpy提供了一个非常底层的函数可以用来生成滑窗:Numpy.lib.stride_tricks.as_stried。
移动滑窗的as_strided实现方法
举一个例子,首先生成一个5000行200列的二维数组,我们需要在这个二维数组上生成一个宽度为200的滑窗,也就是说,第一个窗口包含前0~199行数据,第二个窗口包含1~200行,第三个窗口包含2~201行,以此类推,一共4801组:
In [106]: d = np.random.randint(100, size=(5000,200))如果使用as_strided函数生成上述滑窗,需要用下面的代码,它生成一个三维数组,包括4801组200X200的矩阵,每一组200X200的矩阵代表一组滑窗:
In [107]: %timeit sd = as_strided(d, (4801,200,200), (200*8, 200*8, 8))
5.97 µs ± 33.2 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)我们再尝试一下用for-loop的方法生成一个滑窗检验一下前面生成的滑窗是否正确:
In [108]: %%timeit
...: sd2 = np.zeros((4801,200,200))
...: for i in range(4801):
...: sd2[i] = d[i:i+200]
...:
722 ms ± 98.8 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
In [109]: np.allclose(sd, sd2)
Out[109]: True从上面的代码可以看出,使用as_strided生成一组滑窗,速度竟然是for-loop的十万倍以上!那么as_strided是如何做到的呢?
关于as_strided函数的详细解析
as_strided是怎么回事呢?看它的函数解释:
Signature: as_strided(x, shape=None, strides=None, subok=False, writeable=True)
Docstring:
Create a view into the array with the given shape and strides... warning:: This function has to be used with extreme care, see notes.
Parameters
----------
x : ndarray
Array to create a new.
shape : sequence of int, optional
The shape of the new array. Defaults to "x.shape".
strides : sequence of int, optional
The strides of the new array. Defaults to "x.strides".
subok : bool, optional
If True, subclasses are preserved.
writeable : bool, optional
If set to False, the returned array will always be readonly. Otherwise it will be writable if the original array was. It is advisable to set this to False if possible (see Notes).Returns
-------
view : ndarray
这个函数接受的第一个参数是一个数组,第二个参数是输出的数据shape,第三个参数是stride。要控制数据的输出,shape和stride都非常重要
shape的含义非常简单,就是指输出的数据的行、列、层数,这个参数是一个元组,元组的元素数量等于数组的维度。
而stride的含义就相对复杂一些,其实它的含义是指“步幅”,意思是每一个维度的数据在内存上平移的字节数量。
因为数组在内存中的存放方式是一维线性方式存放的,因此要访问数组中的某个数字就需要知道平移到哪一个内存单元,ndarray通过stride“步幅”来指定这个平移的幅度。
在as_strided函数中,stride也是一个元组,其元素的数量必须跟shape的元素数量相同,每一个元素就代表该维度的每一个数据相对前一个数据的内存间隔。
举个例子:
In [188]: d = np.random.randint(10, size=(5,3))
In [189]: d
Out[189]:
array([[4, 4, 6],
[2, 9, 3],
[5, 1, 1],
[2, 0, 0],
[9, 2, 3]])
| 地址0 | 地址1 | 地址2 | 地址3 | 地址4 | 地址5 | 地址6 | 地址7 | 地址8 | 地址9 | 地址A | 地址B | 地址C | 地址D | 地址E |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 4 | 5 | 2 | 9 | 3 | 5 | 1 | 1 | 2 | 0 | 0 | 9 | 2 | 3 |
我们之所以看到一个二维数组,是因为numpy数组的shape为(5, 3),stride为(24, 8),意思是说,我们看到的数据有5行3列,对应shape的(5, 3),每一行与前一行间隔24个字节(其实就是三个数字,因为每一个int类型占据8字节,而每一列数字比前一列相差8字节(1个数字)
理解上面的含义以后,也就能理解如何生成一个数据滑窗了,如果我们需要生成一个2X3的数据滑窗,在d上滑动,实际上可以生成一个4组,2行3列的数据视图,第一组覆盖d的第0、1两行,第二层覆盖d的第1、2两行,第三层覆盖d的第2、3两行……这样就形成了数据滑窗的效果,我们只要在新的数据视图上遍历,就能遍历整个滑窗。这样做的好处是,在整个遍历的过程中完全不需要对数据进行任何移动或复制的操作,因此速度飞快。
根据上面的思路,我们需要生成一个新的数据视图,其shape为(4, 2, 3)代表4组(从头到尾滑动4次),2行3列(滑窗的尺寸)
接下来需要确定stride,如前所述stride同样是一个包含三个元素的元组,第一个元素是两层数据之间的内存间隔,由于我们的滑窗每滑动一次下移一行,因此层stride应该是平移三个数字,也就是24个字节,行stride和列stride与原来的行列stride一致,因为我们需要原样看到按顺序的数字,因此,新的stride就是:(24, 24, 8)
我们来看看这个新的数据视图是什么样子:
In [190]: as_strided(d, shape=(4,2,3), strides=(24,24,8))
Out[190]:
array([[[4, 4, 6],
[2, 9, 3]],
[[2, 9, 3],
[5, 1, 1]],
[[5, 1, 1],
[2, 0, 0]],
[[2, 0, 0],
[9, 2, 3]]])
看!一个数据滑窗正确地出现了!
使用as_strided函数的危险之处
使用s_strided函数的最大问题是内存读取风险,在as_strided生成新的视图时,由于直接操作内存地址(这一点像极了C的指针操作),而且它并不会检查内存地址是否越界,因此如果稍有不慎,就会读到别的内存地址。关键是,如果不设置可读参数,还能直接对内存中的数据进行操作,这样就带来了无比大的风险。了解这个风险对正确操作至关重要!
例如,使用下面的stride会直接溢出到其他的未知内存地址上,并读取它的值,甚至还可以直接修改它:
In [194]: as_strided(d, shape=(5,2,3), strides=(24,24,8))
Out[194]:
array([[[ 4, 4, 6],
[ 2, 9, 3]],
[[ 2, 9, 3],
[ 5, 1, 1]],
[[ 5, 1, 1],
[ 2, 0, 0]],
[[ 2, 0, 0],
[ 9, 2, 3]],
[[ 9, 2, 3],
[2251799813685248, 18963, 0]]])
这时对象的第五组就映射到了三个未知的内存地址上,如果不慎修改了这三个地址上的内容,就可能造成难以预料的问题,如程序崩溃等。
所以,官方才在文档中郑重地警告:如果有可能,尽量避免使用as_strided函数
以上就是python在numpy上移动窗口的全部内容了,希望能给大家一个参考,也希望大家多多支持W3Cschool。

 免费AI编程助手
免费AI编程助手



