快速排序(Quick Sort)是一种高效的分治排序算法,它以其出色的性能和广泛的应用而闻名。本文将深入讲解快速排序的原理、步骤和时间复杂度,并探讨其优势和应用场景。
快速排序原理
快速排序的核心思想是通过选择一个基准元素,将待排序数组分割为两个子数组,一部分小于基准,一部分大于基准。然后对两个子数组分别进行递归排序,最终将它们合并起来得到有序的结果。
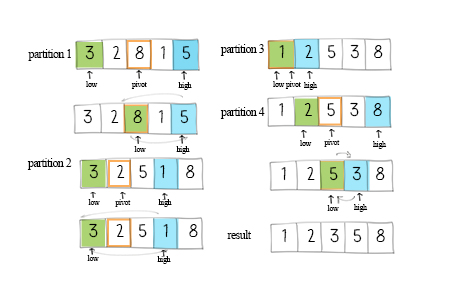
快速排序步骤
具体步骤如下:
- 选择一个基准元素(通常是第一个或最后一个元素)。
- 设定两个指针,一个指向数组的起始位置,一个指向数组的末尾位置。
- 从右向左找到第一个小于基准的元素,从左向右找到第一个大于基准的元素,交换它们的位置。
- 重复步骤3,直到两个指针相遇。
- 将基准元素与指针相遇位置的元素进行交换,此时基准元素位于正确的位置。
- 对基准元素左边和右边的子数组分别进行递归排序,重复上述步骤。
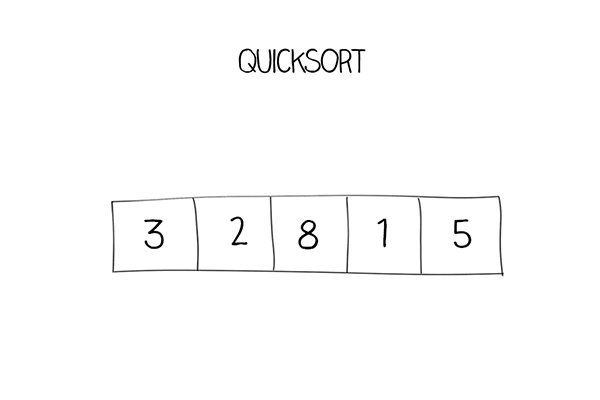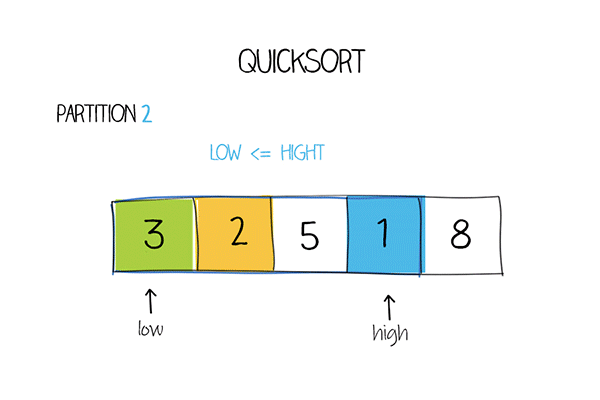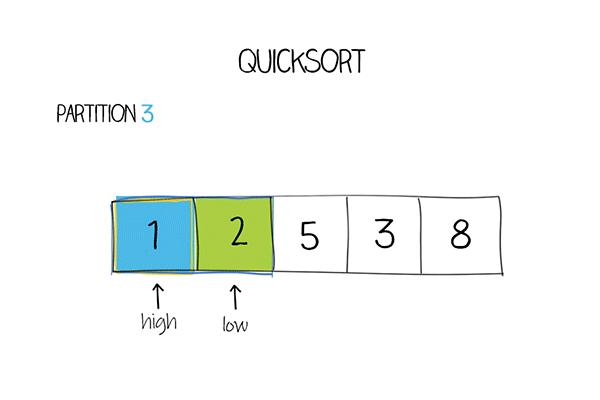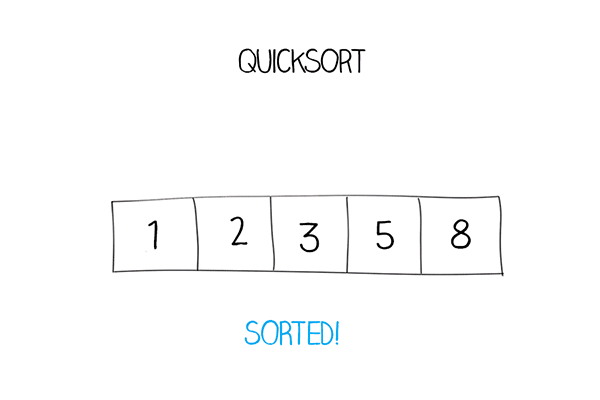
示例代码
public class QuickSort {
public static void quickSort(int[] a, int low, int high) {
// low为起始索引,high为结束索引
int index = partition(a, low, high);
// 对分割后的左半部分进行递归排序
if (low < index-1) quickSort(a, low, index-1);
// 对分割后的左半部分进行递归排序
if (index < high) quickSort(a, index, high);
}
private static int partition(int[] a, int low, int high) {
// 将数组a根据基准元素进行分割,并返回分割后基准元素的索引
int mid = low + (high-low)/2;// 计算数组的中间位置
int pivot = a[mid]; // 选择中间位置的元素作为基准元素
while (low <= high) {
// 在基准元素左边找到第一个大于等于基准元素的元素的索引
while (a[low] < pivot) low ++;
// 在基准元素右边找到第一个小于等于基准元素的元素的索引 while (a[high] > pivot) high --;
// 若找到的两个元素的索引仍满足low<=high,则交换两个元素的位置
if (low <= high) {
swap(a, low, high);
low ++;
high --;
}
}
// 返回基准元素的索引,用于后续的递归排序
return low;
}
// 交换数组两个元素的位置
private static void swap(int[] a, int i, int j) {
int tmp = a[i];
a[i] = a[j];
a[j] = tmp;
}
}时间复杂度
快速排序的平均时间复杂度为O(nlogn),其中n为待排序数组的长度。这是因为每次分割都将数组划分为大致相等的两部分,而递归的深度为logn。在最坏情况下,如果每次划分都不平衡,时间复杂度可能达到O(n^2)。
为了避免最坏情况的发生,可以采用一些优化策略,如随机选择基准元素或使用三数取中法来选择基准元素,以提高算法的性能和稳定性。
快速排序的优势
快速排序具有以下优势:
- 高效性能:平均情况下,快速排序是最快的排序算法之一,尤其适用于大规模数据的排序。
- 原地排序:快速排序可以在原始数组上进行排序,不需要额外的空间。
- 适应性:快速排序在处理部分有序数组时仍然具有较好的性能。
总结
快速排序是一种高效的分治排序算法,通过选择基准元素和不断划分子数组来实现排序。它具有优秀的性能和广泛的应用场景,特别适合处理大规模数据集。了解快速排序的原理和步骤,以及掌握优化策略,可以帮助开发人员选择合适的算法,并编写出高效的排序代码。

 免费AI编程助手
免费AI编程助手



