堆排序：理解原理与实现

堆排序是一种高效的排序算法，基于堆数据结构实现。它具有稳定的时间复杂度，并且适用于大规模数据集的排序。本文将详细讲解堆排序算法的原理、步骤，并提供Java实现示例代码，帮助读者深入理解和实践堆排序。

堆排序概述

什么是堆？

堆是一种完全二叉树的数据结构，具有以下特性：
- 最大堆：父节点的键值大于或等于其子节点的键值。
- 最小堆：父节点的键值小于或等于其子节点的键值。
堆排序的原理

堆排序利用最大堆或最小堆的性质进行排序。它的基本思想是将待排序的数组构建成一个最大堆（或最小堆），然后逐步将堆顶元素与最后一个元素交换，再对剩余元素进行堆调整，重复该过程直到整个数组有序。

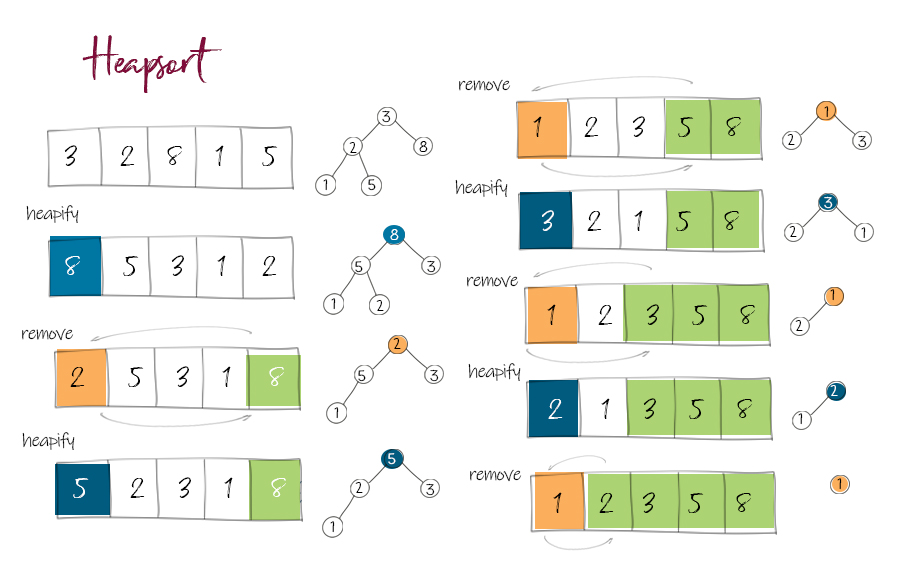
heapsort

堆排序步骤

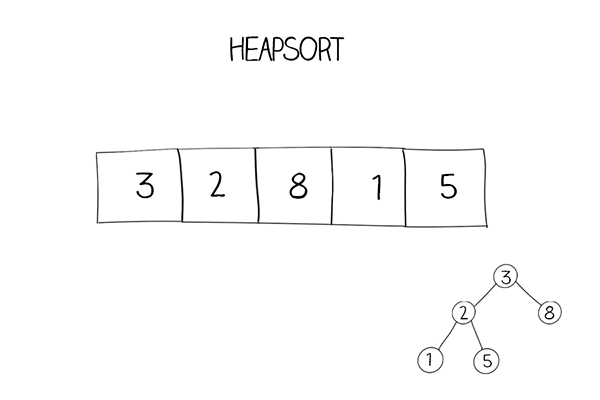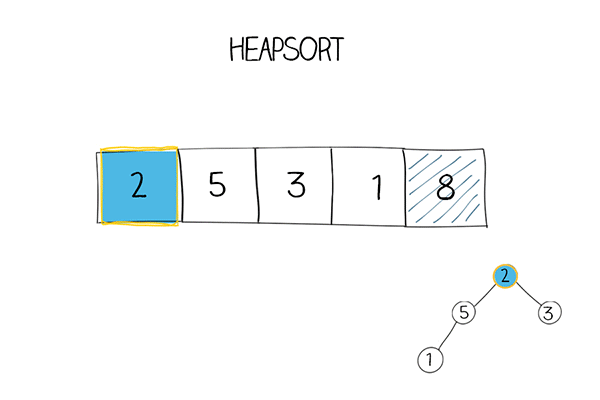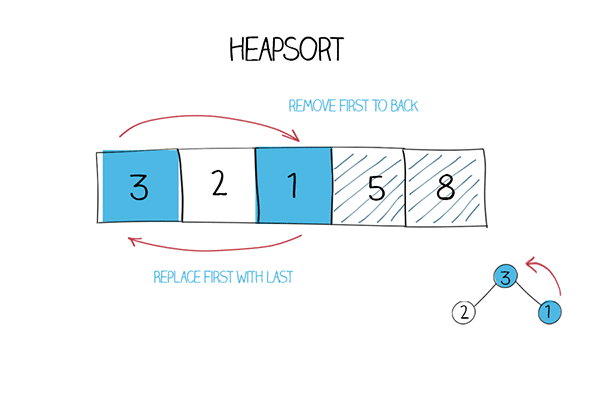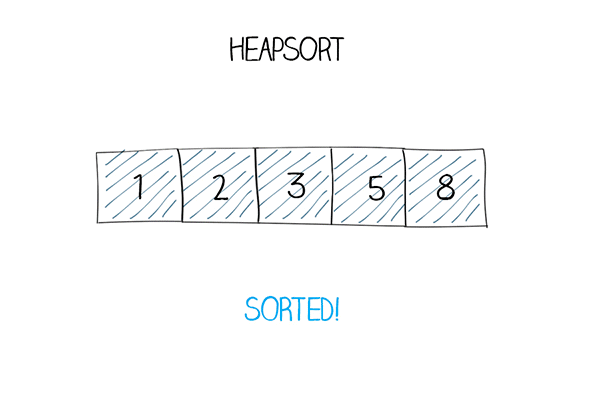
构建最大堆（或最小堆）将待排序数组转换为最大堆（或最小堆），确保父节点的键值大于或等于（或小于或等于）其子节点的键值。可以从最后一个非叶子节点开始，依次向上进行堆调整。
交换堆顶元素将堆顶元素与最后一个元素交换，将最大（或最小）元素移至数组末尾。
调整堆对剩余元素进行堆调整，保持堆的性质。
重复步骤2和步骤3重复执行步骤2和步骤3，直到所有元素都排好序。

heapsort-600

示例代码

下面是使用Java语言实现堆排序的示例代码：

public class HeapSort {
    public static void heapSort(int[] arr) {
        int n = arr.length;

        // 构建最大堆
        for (int i = n / 2 - 1; i >= 0; i--)
            heapify(arr, n, i);

        // 交换堆顶元素与末尾元素，并调整堆
        for (int i = n - 1; i > 0; i--) {
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;

            heapify(arr, i, 0);
        }
    }

    private static void heapify(int[] arr, int n, int i) {
        int largest = i; // 初始化最大元素索引
        int left = 2 * i + 1; // 左子节点索引
        int right = 2 * i + 2; // 右子节点索引

        // 比较左子节点与根节点
        if (left < n && arr[left] > arr[largest])
            largest = left;

        // 比较右子节点与当前最大值
        if (right < n && arr[right] > arr[largest])
            largest = right;

        // 如果最大值不是根节点，则交换并继续调整堆
        if (largest != i) {
            int temp = arr[i];
            arr[i] = arr[largest];
            arr[largest] = temp;

            heapify(arr, n, largest);
        }
    }

    public static void main(String[] args) {
        int[] arr = { 3, 2, 8, 1, 5};
        heapSort(arr);

        System.out.println("排序结果：");
        for (int num : arr)
            System.out.print(num + " ");
    }
}

堆排序的时间复杂度与稳定性

时间复杂度：构建堆的时间复杂度是O(n)，交换堆顶元素并调整堆的时间复杂度是O(log n)，总体时间复杂度是O(n log n)；
稳定性：堆排序是一种不稳定的排序算法，因为在交换堆顶元素和末尾元素的过程中，可能改变相同元素的相对顺序。

总结

堆排序是一种高效的排序算法，适用于大规模数据集的排序。通过构建最大堆（或最小堆）和不断交换堆顶元素并调整堆的过程，可以实现对数组的排序。Java示例代码提供了一个简单的实现，并且通过深入解析堆排序的原理和步骤，读者可以更好地理解和运用堆排序算法。