在计算机科学中,搜索是一项基本而重要的操作。对于有序数据,二分查找算法是一种高效的搜索方法。本文将介绍二分查找算法的原理、实现以及其在实际应用中的优势,帮助读者理解和应用这一常用的搜索算法。
什么是二分查找算法?
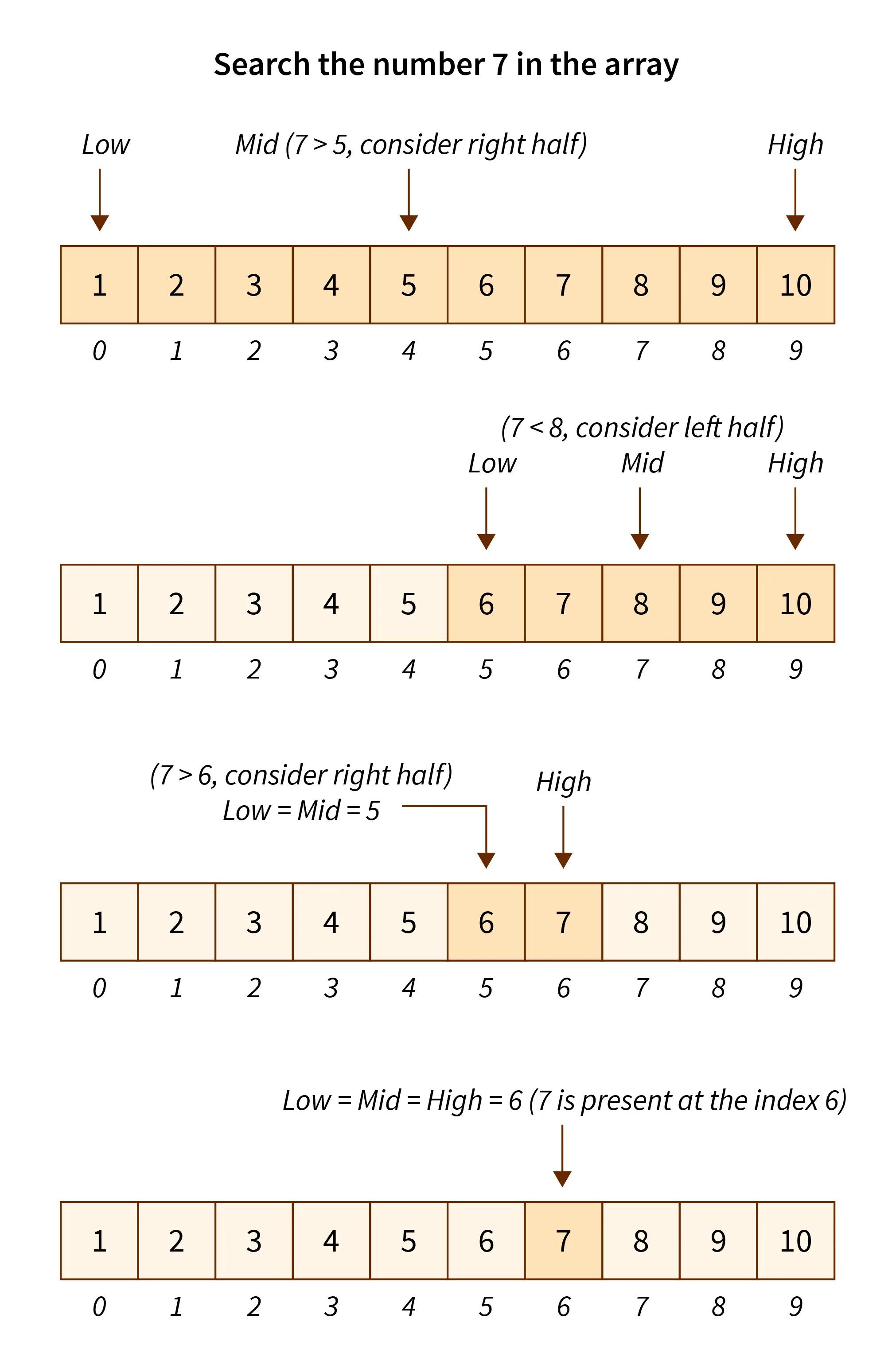
二分查找算法,也称为折半查找算法,是一种在有序数据集合中查找目标值的算法。它通过将目标值与数据集合的中间元素进行比较,从而将搜索范围缩小一半。如果目标值等于中间元素,则找到了目标;如果目标值小于中间元素,则在左半部分继续查找;如果目标值大于中间元素,则在右半部分继续查找。通过重复这个过程,最终可以找到目标值或确定目标值不存在于数据集合中。
二分查找算法的实现
public class BinarySearch {
public static int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
}在binarySearch方法中,我们使用了两个指针left和right来表示搜索范围的左右边界。在每次循环中,计算中间元素mid并与目标值进行比较。如果中间元素等于目标值,则找到了目标,返回其索引。如果中间元素小于目标值,则目标值可能在右半部分,将left指针更新为mid + 1。如果中间元素大于目标值,则目标值可能在左半部分,将right指针更新为mid - 1。通过不断缩小搜索范围,最终可以找到目标值或确定目标值不存在。
二分查找算法的优势
二分查找算法具有以下几个优势:
- 高效的时间复杂度:二分查找算法的时间复杂度为O(log n),其中n是数据集合的大小。相比于线性搜索算法的O(n)时间复杂度,二分查找算法在大数据集合中的搜索效率更高。它通过每次将搜索范围缩小一半,快速逼近目标值,减少了搜索的次数。
- 适用于有序数据:二分查找算法要求数据集合是有序的,但正是由于这一特性,它才能发挥出高效的搜索能力。在实际应用中,许多数据集合都是有序的,如数组、数据库索引等。二分查找算法可以快速定位目标值所在的位置,提高搜索效率。
- 简单而易实现:二分查找算法的实现相对简单,只需熟悉基本的循环和条件判断即可。它不依赖于复杂的数据结构或算法思想,使得开发人员能够轻松理解和应用。
二分查找算法的应用
二分查找算法在许多实际应用中得到广泛应用,包括但不限于以下几个方面:
- 数组搜索:对于有序数组,可以使用二分查找算法快速搜索目标值的位置。例如,在大型的升序数组中查找特定元素或确定元素是否存在。
- 数据库索引:数据库中的索引通常是有序的,通过使用二分查找算法可以快速定位满足特定条件的数据行。这提高了数据库查询的效率,减少了搜索时间。
- 字典搜索:在字典或词典中,单词通常是按字母顺序排列的。使用二分查找算法可以快速找到特定单词,或者在给定前缀的情况下找到以该前缀开头的所有单词。
- 游戏开发:在游戏开发中,二分查找算法可以应用于各种场景,如查找特定物品的位置、确定游戏进度等。通过快速查找和定位,可以提供更好的游戏体验。
总结
二分查找算法是一种高效且常用的搜索算法,适用于有序数据集合中的搜索操作。它通过每次将搜索范围缩小一半,快速逼近目标值,具有较低的时间复杂度和简单的实现方式。在实际应用中,二分查找算法在数组搜索、数据库索引、字典搜索和游戏开发等领域发挥着重要作用。通过了解和掌握二分查找算法,我们可以更高效地搜索和处理有序数据,提高算法的效率和性能。

 免费AI编程助手
免费AI编程助手



