布隆过滤器：高效快速的数据查找与去重工具

在计算机科学领域中，布隆过滤器是一种高效的数据结构，用于快速判断一个元素是否存在于一个大规模数据集中。它具有快速查找和去重的特性，广泛应用于各种领域，如缓存系统、网络爬虫、数据库查询等。本文将解释布隆过滤器的工作原理、优势和应用场景。

布隆过滤器的工作原理

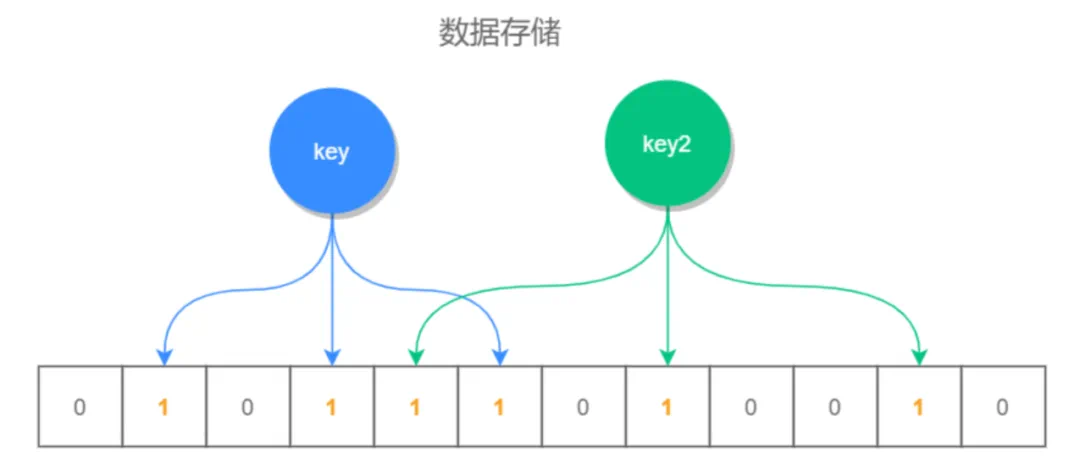
布隆过滤器是由布隆提出的一种数据结构，基于位数组和一组哈希函数构成。它的基本思想是通过多个哈希函数将元素映射到位数组的不同位置上，每个位置对应一个位值（通常为0或1）。当一个元素被插入到布隆过滤器中时，对应位置的位值被置为1。当需要判断一个元素是否存在时，将元素经过相同的哈希函数映射，并检查对应位置的位值，如果所有位置的位值都为1，则说明元素可能存在，否则元素一定不存在。

布隆过滤器的优势

• 高效的查找操作：布隆过滤器通过哈希函数的快速映射和位数组的高效访问，可以在常数时间内判断一个元素是否存在，无需遍历整个数据集。
• 节省存储空间：布隆过滤器使用位数组来表示数据集的存在性，所占用的存储空间相对较小。通过调整位数组的大小和哈希函数的个数，可以在存储空间和误判率之间进行权衡。
• 高效的去重功能：由于布隆过滤器可以快速判断元素是否存在，因此可以有效地去重，避免将重复的数据插入到数据集中。

布隆过滤器的应用场景

布隆过滤器在以下场景中得到广泛应用：

• 缓存系统：布隆过滤器可以用于快速判断一个数据是否已经存在于缓存中，从而避免不必要的查询操作，提高系统的响应速度。
• 网络爬虫：布隆过滤器可以用于记录已经访问过的URL，以避免重复爬取相同的页面，提高爬虫的效率。
• 数据库查询优化：布隆过滤器可以用于快速判断某个数据是否存在于数据库中，从而减少不必要的查询操作，提高查询效率。
• 邮件服务器：布隆过滤器可以用于过滤垃圾邮件，快速判断一个邮件是否是垃圾邮件，从而提高邮件过滤的效率。

布隆过滤器的注意事项

• 布隆过滤器存在一定的误判率，即可能将不存在的元素误判为存在。误判率取决于位数组的大小和哈希函数的个数，可以通过调整这些参数来控制误判率。
• 布隆过滤器不支持删除操作，因为删除一个元素可能会影响其他元素的判断结果。如果需要支持删除操作，可以使用其他变种的布隆过滤器，如计数布隆过滤器。

总结

布隆过滤器是一种高效快速的数据查找与去重工具，通过哈希函数和位数组的结合，实现了常数时间内的元素判断。它具有高效的查找操作、节省存储空间和高效的去重功能等优势，并在缓存系统、网络爬虫、数据库查询优化和垃圾邮件过滤等领域得到广泛应用。然而，布隆过滤器也存在误判率和不支持删除操作的限制。在使用布隆过滤器时，需要根据具体场景和需求合理设置参数，并注意处理误判率和删除操作的问题。布隆过滤器是一种强大的数据结构，可以为大规模数据集的查找和去重提供高效的解决方案。