斐波那契数列是一种经典的数学序列,它的规律是每一项都等于前两项之和,例如:1, 1, 2, 3, 5, 8, 13, 21, ...。斐波那契数列在计算机科学中有很多应用,比如算法分析、数据结构设计、密码学等。本文将介绍如何用c语言编写一个高效的斐波那契数列生成器,以及分析其时间和空间复杂度。
一种最简单的方法是用递归函数来实现斐波那契数列,代码如下: c //递归函数,返回第n项斐波那契数 int fib(int n) { //递归终止条件 if (n == 1 || n == 2) { return 1; } //递归调用 return fib(n - 1) + fib(n - 2); }
这种方法的优点是代码简洁易懂,但是缺点是效率很低,因为它会重复计算很多已经计算过的子问题,导致指数级的时间复杂度。例如,要计算fib(5),就需要先计算fib(4)和fib(3),而要计算fib(4),又需要先计算fib(3)和fib(2),这样就造成了很多重复的工作。可以用一棵递归树来表示这种过程:
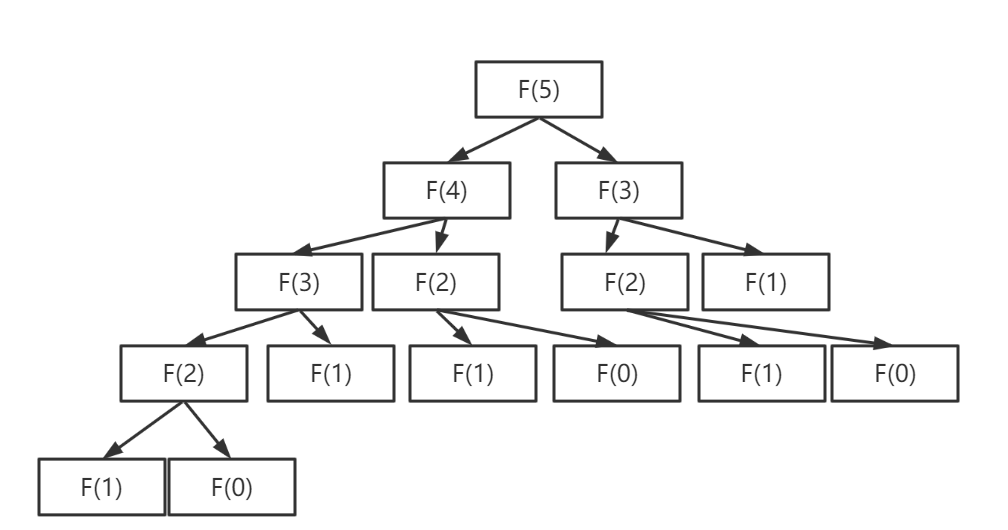
从图中可以看出,递归树的节点数是指数级增长的,所以这种方法的时间复杂度是O(2^n),空间复杂度是O(n),其中n是斐波那契数列的项数。
为了提高效率,我们可以用动态规划的思想来优化这个问题。动态规划的核心是把一个大问题分解成若干个小问题,并且记录下每个小问题的解,避免重复计算。对于斐波那契数列,我们可以用一个数组来存储每一项的值,然后从第三项开始,利用前两项的值来计算当前项的值,代码如下:
```c
//动态规划函数,返回第n项斐波那契数
int fib(int n) {
//创建一个数组,大小为n+1,用来存储每一项的值
int* arr = (int*)malloc(sizeof(int) * (n + 1));
//初始化数组的前两项为1
arr[1] = 1;
arr[2] = 1;
//从第三项开始,利用前两项的值来计算当前项的值,并存入数组中
for (int i = 3; i <= n; i++) {
arr[i] = arr[i - 1] + arr[i - 2];
}
//返回数组中第n项的值
int result = arr[n];
//释放数组空间
free(arr);
return result;
}这种方法的优点是效率很高,因为它只需要遍历一次数组就可以得到结果,而且不会重复计算任何子问题。所以这种方法的时间复杂度是O(n),空间复杂度也是O(n)。
不过,我们还可以进一步优化空间复杂度。我们注意到,在计算当前项的值时,我们只需要知道前两项的值,而不需要知道之前所有的值。所以我们可以用两个变量来存储前两项的值,而不需要用一个数组来存储所有的值,代码如下:
//空间优化函数,返回第n项斐波那契数
int fib(int n) {
//创建两个变量,分别存储前两项的值,初始为1
int a = 1;
int b = 1;
//从第三项开始,利用前两项的值来计算当前项的值,并更新前两项的值
for (int i = 3; i <= n; i++) {
//计算当前项的值
int c = a + b;
//更新前两项的值
a = b;
b = c;
}
//返回最后一项的值
return b;
}这种方法的优点是空间复杂度降低为O(1),因为它只需要两个变量来存储前两项的值,而不需要额外的数组空间。时间复杂度仍然是O(n)。
综上所述,我们介绍了三种用c语言编写斐波那契数列生成器的方法,分别是递归、动态规划和空间优化。其中,递归方法虽然简单,但是效率很低,时间复杂度是O(2^n),空间复杂度是O(n)。动态规划方法可以提高效率,时间复杂度是O(n),空间复杂度也是O(n)。空间优化方法可以进一步降低空间复杂度,时间复杂度仍然是O(n),空间复杂度是O(1)。因此,如果要编写一个高效的斐波那契数列生成器,我们推荐使用空间优化方法。
C语言相关课程推荐C语言相关课程

 免费AI编程助手
免费AI编程助手



