在计算机科学中,数据的压缩和编码是一个重要的研究领域。而哈夫曼树作为一种经典的数据结构,以其独特的构建方式和高效的编码方式在数据压缩和编码中发挥着重要作用。本文将介绍哈夫曼树的原理、构建方法以及在数据压缩和编码中的应用,帮助读者深入理解这一精妙的数据结构。
哈夫曼树简介
哈夫曼树是一种特殊的二叉树,它通过一种被称为哈夫曼编码的方式来表示数据。哈夫曼编码是一种可变长度编码方式,根据数据的频率进行编码,使得出现频率高的数据用较短的编码表示,而出现频率低的数据用较长的编码表示,从而实现数据的高效压缩和解压缩。
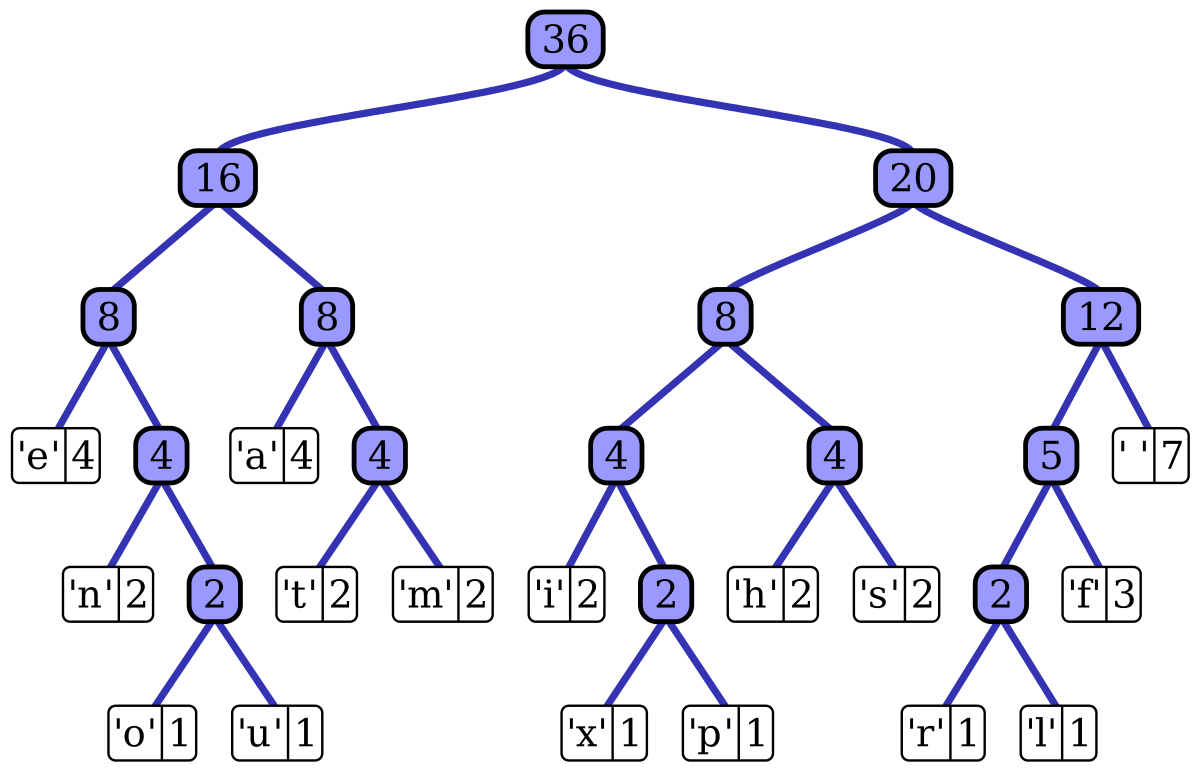
哈夫曼树的构建
哈夫曼树的构建过程包括以下几个步骤:
- 统计字符频率:首先需要统计待编码的数据中每个字符出现的频率,可以通过扫描数据集合或文件来实现。
- 构建哈夫曼树:根据字符频率构建哈夫曼树的过程是一个贪心算法,它通过不断合并频率最低的两个节点来构建树。具体步骤如下:将每个字符作为一个独立的节点,将它们的频率作为节点权值。从节点集合中选择两个频率最低的节点,创建一个新的节点作为它们的父节点,父节点的权值为子节点权值之和。将新节点加入节点集合,同时从集合中删除原来的两个子节点。重复以上步骤,直到节点集合中只剩下一个节点,这个节点就是哈夫曼树的根节点。
- 构建编码表:根据哈夫曼树,可以生成每个字符对应的哈夫曼编码。从根节点出发,向左走为0,向右走为1,直到叶子节点,将路径上的0和1分别对应于左子树和右子树,即得到对应的编码。将字符与其编码建立映射关系,即可构建编码表。
哈夫曼树的应用
哈夫曼树在数据压缩和编码中具有广泛的应用,主要有以下两个方面:
- 数据压缩:哈夫曼树可以根据字符的频率构建出高效的编码方式,将频率较高的字符用较短的编码表示,从而实现数据的压缩。在压缩过程中,通过哈夫曼树将原始数据转换为对应的哈夫曼编码,从而减少数据的存储和传输空间。
- 数据编码:哈夫曼树还可以用于数据的编码和解码。在编码过程中,根据字符与编码表的映射关系,将原始数据转换为哈夫曼编码。在解码过程中,根据哈夫曼树和哈夫曼编码,将编码还原为原始数据。通过哈夫曼编码,可以实现高效的数据传输和存储。
总结
哈夫曼树作为一种高效的数据结构,在数据压缩和编码中发挥着重要作用。通过统计字符频率和贪心算法构建哈夫曼树,可以生成高效的编码方式,实现数据的压缩和解压缩。哈夫曼树广泛应用于数据压缩、通信传输、文件存储等领域,为我们提供了一种精妙的数据压缩和编码的解决方案。通过深入理解哈夫曼树的原理和构建方法,我们可以更好地应用它来解决实际问题,提高数据处理的效率和性能。

 免费AI编程助手
免费AI编程助手



